Non tutte le Funzioni escono col buco

Abbiamo viso il limite l finito per una funzione e x che tende a un numero finito .
si può parlare anche di limite infinito?
e si può parlare di limite per $x\rightarrow \infty$ ?

Sì e Sì

Per parlare di tutti questi casi con una sola definizione utilizziamo

La Definizione Topologica di Limite

$\left\{\lim_{x\rightarrow x_o}{f(x)}=l\right\} \Leftrightarrow \Big\lbrace \forall J(l) \; \exists \; I(x_o) \;|\; \forall x \in I(x_o) \Rightarrow f(x) \in J(l)\Big\}$

e si legge:

Si dice che il limite della funzione per che tende a è
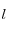
se e solo se
per ogni intorno di esiste un intorno di
tale che
per ogni appartenente all’intorno di
appartiene all’intorno di

Il concetto è quello che abbiamo intuitivamente già compreso: quando la si avvicina a un certo valore , la si avvicina al valore limite

Questa definizione, oltre il caso già visto in cui e sono numeri reali finiti, usando il linguaggio degli intorni, comprende i casi per $x \rightarrow \infty$ e i casi per limite $\infty$ che vedremo fra poco.

Limiti infiniti
per x che tende a infinito

se prendiamo la funzione

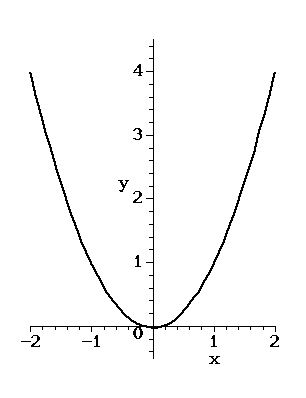(una semplice parabola) per x che cresce anche la y cresce indefinitamente; ovvero quando x è in un intorno di infinito, anche y entra in un intorno di infinito

per x che tende a Ma il limite può essere infinito anche per x che tende a un numero finito:

Ad esempio [...]

limite finito per x che tende a infinito
Quando invece, per $x\rightarrow\infty$ , si ha un limite finito, abbiamo i ben noti [1] asintoti orizzontali.

L’esempio è quello dell’iperbole

$y=\frac{1}{|x|}$

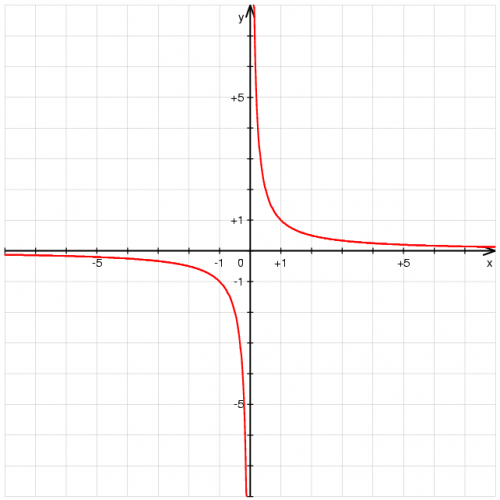
per cui:

$\lim_{x\rightarrow \infty}{\frac{1}{x}}=0$

Inoltre, in questi casi, si dice che la funzione ha un asintoto [2] orizzontale .

Una funzione ammette sempre un limite?
Quando si procede al calcolo di un limite, si trova sempre un risultato, che esso sia un numero finito o l’infinito?

NO

In alcuni casi il limite non esiste.

Ad esempio la funzione y=sen(x) non ammette limite per 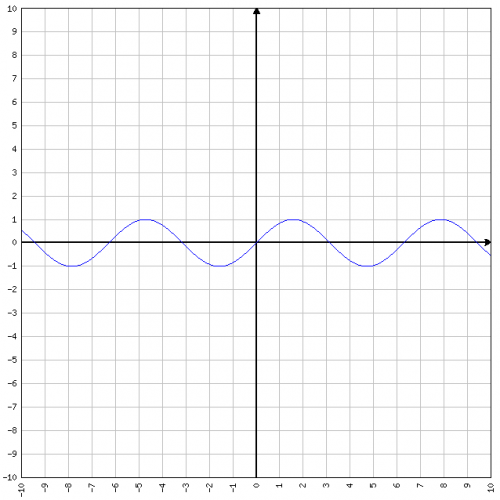$x\rightarrow\infty$ . Infatti per quanto x cresca, la y continua a oscillare tra 1 e -1 e non si avvicina a nessun numero.

Esistono casi in cui il limite non esiste anche per $x\rightarrow x_o$ finito?
SÌ

Questo avviene quando, per un certo valore di x la funzione fa un ’salto’:

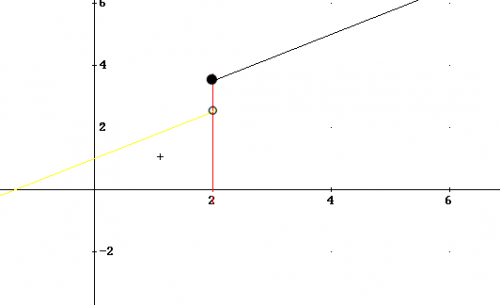
Ma il grafico qui sopra è il grafico di una funzione?

SI

e per di più una funzione biunivoca: a ogni valore della x corrisponde uno e un solo valore della y.

L’espressione della funzione è un po’ particolare: si dice definita pe "casi"

$y=f(x)=\left\{\begin{matrix} \frac{3}{4} x +2 , & \mbox{se }x\ge 2 \\ \frac{3}{4} x +1 , & \mbox{se }x < 2 \end{matrix}\right.$

Per $x\rightarrow 2$ questa funzione NON ammette limite: infatti quando x si avvicina a 2 la y si avvicina a due numeri differenti se ci stiamo avvicinando da destra (numeri più grandi di due) o da sinistra. Nel primo caso y si avvicina a 7/2 e nel secondo a 5/2.

Eppure, quando x si avvicina a 2 da sinistra, cioè con numeri più piccoli di 2, la y si avvicina quanto si vuole a 5/2. Si può parlare allora di limite sinistro

Se ci stiamo avvicinando da destra (numeri più grandi di due) y si avvicina a 7/2: questo si chiamerà limite destro

se esiste il limite per $x\rightarrow x_o$ ALLORA esistono limite destro e sinistro.
NON è vero il viceversa

Quando esiste il limite finito di una funzione per $x\rightarrow x_o \in \Real$ si dice che la funzione è continua in

Definizione di funzione continua

Si dice che una funzione per $x\rightarrow x_o \in \Re$
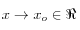
se e solo se
ESISTE E esiste finito il limite per $x\rightarrow x_o$ e coincide con .

Il primo esempio che abbiamo fatto sul limite di una funzione, quello del calcolo della velocità istantanea come limite della velocità media per $\Delta t \rightarrow 0$ è il caso di una funzione discontinua: in $\Delta t = 0$ infatti la funzione velocità media non esiste, e quindi è violata la prima condizione di continuità, mentre come abbiamo visto il limite esiste.
Il grafico era quello di una retta con un ’buco’ per $\Delta t = 0$

Sopra abbiamo visto 3 casi in cui la funzione NON è continua:

il caso in cui la funzione fa un salto si chiama discontinuità di I specie, ed è quello in cui esiste 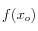ma non il limite
il caso in cui c’è un asintoto verticale si chiama discontinuità di II specie, ed è quello in cui NON esiste 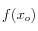e il limite è INFINITO
il caso in cui c’è un ’buco’ si chiama discontinuità di III specie, ed è quello in cui NON esiste 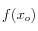MA ESISTE il limite FINITO per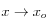 $x\rightarrow x_o$

In tutti questi casi le funzioni non sono continue e infatti, per disegnarle, siamo costretti a staccare la penna dal foglio

Generalmente le funzioni che studiamo sono continue o continue a tratti, ma possono esistere funzioni molto "strane"

Ad esempio la funzione di Dirichlet è una funzione che ha come dominio tutto $\Re$ ma che non è continua in nessun punto:

$y=f(x)=\left\{\begin{matrix} 1 & \mbox{se x è numero razionale} \\ 0 & \mbox{se x è numero irrazionale} \end{matrix}\right.$

Siccome intorno a un numero razionale ve ne sono infiniti irrazionali e viceversa questa funzione salta in ogni suo punto da zero a uno, e non esiste mai il limite

SOMMARIO
Limiti infiniti
Limiti per $x \rightarrow \infty$
Asintoti
Funzione continua
Discontinuità di prima specie: limite destro e sinistro
Discontinuità di seconda specie
Discontinuità di terza specie